Advanced Mathematics

上溢

下溢

病态条件

基于梯度优化

目标函数/代价函数/损失函数/误差函数

局部极小点/局部极大点/全局最小点

梯度

学习率

Jacobian Matrix & Hessian Matrix

凸优化

最成功的特定优化领域或许是 凸优化(Convex optimization)。凸优化通过更强 的限制提供更多的保证。凸优化算法只对凸函数适用，即 Hessian 处处半正定的函 数。因为这些函数没有鞍点而且其所有局部极小点必然是全局最小点，所以表现很 好。然而，深度学习中的大多数问题都难以表示成凸优化的形式。凸优化仅用作一 些深度学习算法的子程序。

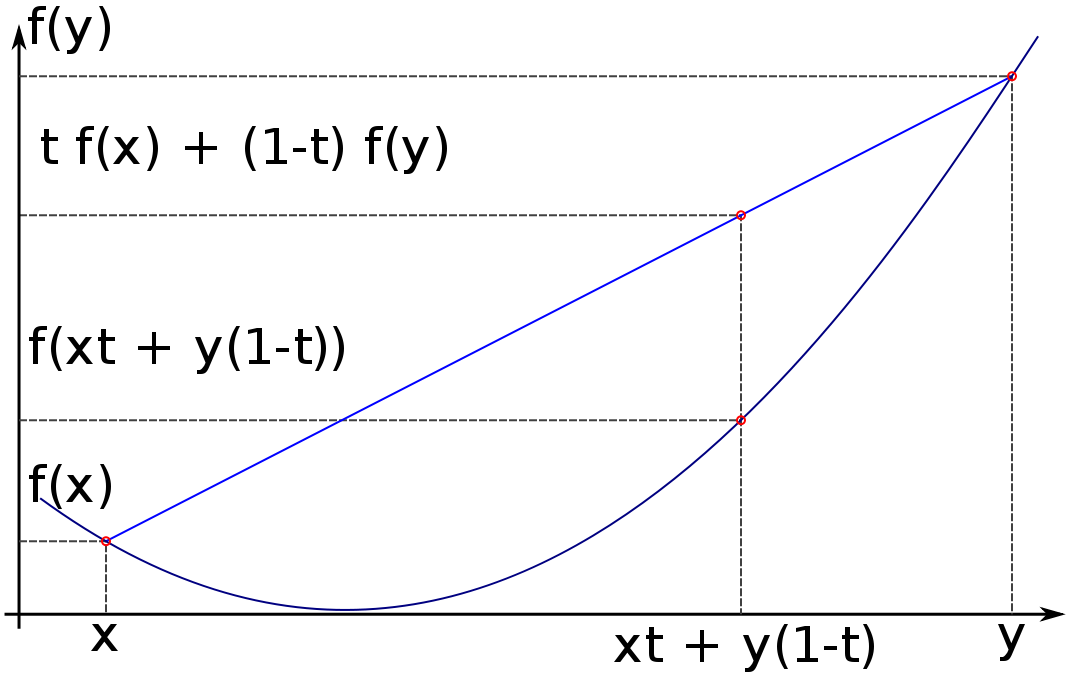
凸函数:f(tx+(1-t)y)<=tf(x)+(1-t)f(y) 0<=t<=1

约束优化

有时候，在 x 的所有可能值下最大化或最小化一个函数 f(x) 不是我们所希望 的。相反，我们可能希望在 x 的某些集合 S 中找 f(x) 的最大值或最小值。这被称 为 约束优化(constrained optimization)。

（注意，这里的x是一个广义上的未知量而不是我们之前在线性回归模型等方法中使用的Dataset的input，这里的x表示为w或者theta都更加合适）

KKT方法

Basic Machine Learning Methods

学习算法

任务T

机器学习任务定义为机器学习系统应该如何处理 样本(example)。样本是 指我们从某些希望机器学习系统处理的对象或事件中收集到的已经量化的 特征 (feature)的集合。

一些常见的机器学习任务列举：

分类/输入缺失分类/回归/转录/机器翻译/结构化输出/合成采样/缺失值填补/去噪/…

性能度量P

对于诸如分类、缺失输入分类和转录任务，我们通常度量模型的 准确率(accu- racy)。准确率是指该模型输出正确结果的样本比率。我们也可以通过 错误率(error rate)得到相同的信息。

通常，我们会更加关注机器学习算法在未观测数据上的性能如何，因为这将决 定其在实际应用中的性能。因此，我们使用 测试集(test set)数据来评估系统性能， 将其与训练机器学习系统的训练集数据分开。

经验E

根据学习过程中的不同经验，机器学习算法可以大致分类为 无监督(unsuper- vised)算法和 监督(supervised)算法。

本书中的大部分学习算法可以被理解为在整个 数据集(dataset)上获取经验。 数据集是指很多样本组成的集合，如第 5.1.1 节所定义的。有时我们也将样本称为 数 据点(data point)。

无监督学习算法(unsupervised learning algorithm)训练含有很多特征的数据 集，然后学习出这个数据集上有用的结构性质。在深度学习中，我们通常要学习生成数据集的整个概率分布，显式地，比如密度估计，或是隐式地，比如合成或去噪。 还有一些其他类型的无监督学习任务，例如聚类，将数据集分成相似样本的集合。

监督学习算法(supervised learning algorithm)训练含有很多特征的数据集，不 过数据集中的样本都有一个 标签(label)或 目标(target)。

大致说来，无监督学习涉及到观察随机向量 x 的好几个样本，试图显式或隐式 地学习出概率分布 p(x)，或者是该分布一些有意思的性质;而监督学习包含观察随 机向量 x 及其相关联的值或向量 y，然后从 x 预测 y，通常是估计 p(y | x)。术语 监 督学习(supervised learning)源自这样一个视角，教员或者老师提供目标 y 给机器学习系统，指导其应该做什么。在无监督学习中，没有教员或者老师，算法必须学会在没有指导的情况下理解数据。

数据表示

大部分机器学习算法简单地训练于一个数据集上。数据集可以用很多不同方式 来表示。在所有的情况下，数据集都是样本的集合，而样本是特征的集合。

表示数据集的常用方法是 设计矩阵(design matrix)。设计矩阵的每一行包含 一个不同的样本。每一列对应不同的特征。

容量

机器学习的主要挑战是我们的算法必须能够在先前未观测的新输入上表现良好， 而不只是在训练集上表现良好。在先前未观测到的输入上表现良好的能力被称为 泛 化(generalization)。

通常情况下，当我们训练机器学习模型时，我们可以使用某个训练集，在训练 集上计算一些被称为 训练误差(training error)的度量误差，目标是降低训练误差。 目前为止，我们讨论的是一个简单的优化问题。机器学习和优化不同的地方在于，我 们也希望 泛化误差 (generalization error)(也被称为 测试误差(test error))很低。 泛化误差被定义为新输入的误差期望。这里，期望的计算基于不同的可能输入，这 些输入采自于系统在现实中遇到的分布。

训练集和测试集数据通过数据集上被称为 数据生成过程(data generating pro- cess)的概率分布生成。通常，我们会做一系列被统称为 独立同分布假设(i.i.d. assumption)的假设。该假设是说，每个数据集中的样本都是彼此 相互独立的(independent)，并且训练集和测试集是 同分布的(identically distributed)，采样自相 同的分布。这个假设使我们能够在单个样本的概率分布描述数据生成过程。然后相 同的分布可以用来生成每一个训练样本和每一个测试样本。我们将这个共享的潜在 分布称为 数据生成分布(data generating distribution)，记作 p_data。这个概率框架 和独立同分布假设允许我们从数学上研究训练误差和测试误差之间的关系。

我们能观察到训练误差和测试误差之间的直接联系是，随机模型训练误差的期 望和该模型测试误差的期望是一样的。假设我们有概率分布 p(x, y)，从中重复采样 生成训练集和测试集。对于某个固定的 w，训练集误差的期望恰好和测试集误差的 期望一样，这是因为这两个期望的计算都使用了相同的数据集生成过程。这两种情 况的唯一区别是数据集的名字不同。

因此我们有两个因素来决定一个学习算法的好坏

降低训练误差-欠拟合（underfitting）

缩小训练误差和测试误差的差距-过拟合（overfitting）

通过调整模型的 容量(capacity)，我们可以控制模型是否偏向于过拟合或者欠 拟合。通俗地，模型的容量是指其拟合各种函数的能力。容量低的模型可能很难拟 合训练集。容量高的模型可能会过拟合，因为记住了不适用于测试集的训练集性质。

一种控制训练算法容量的方法是选择 假设空间(hypothesis space)，即学习算 法可以选择为解决方案的函数集。例如，线性回归算法将关于其输入的所有线性函 数作为假设空间。广义线性回归的假设空间包括多项式函数，而非仅有线性函数。这 样做就增加了模型的容量。

统计学习理论中最重要 的结论阐述了训练误差和泛化误差之间差异的上界随着模型容量增长而增长，但 随着训练样本增多而下降。

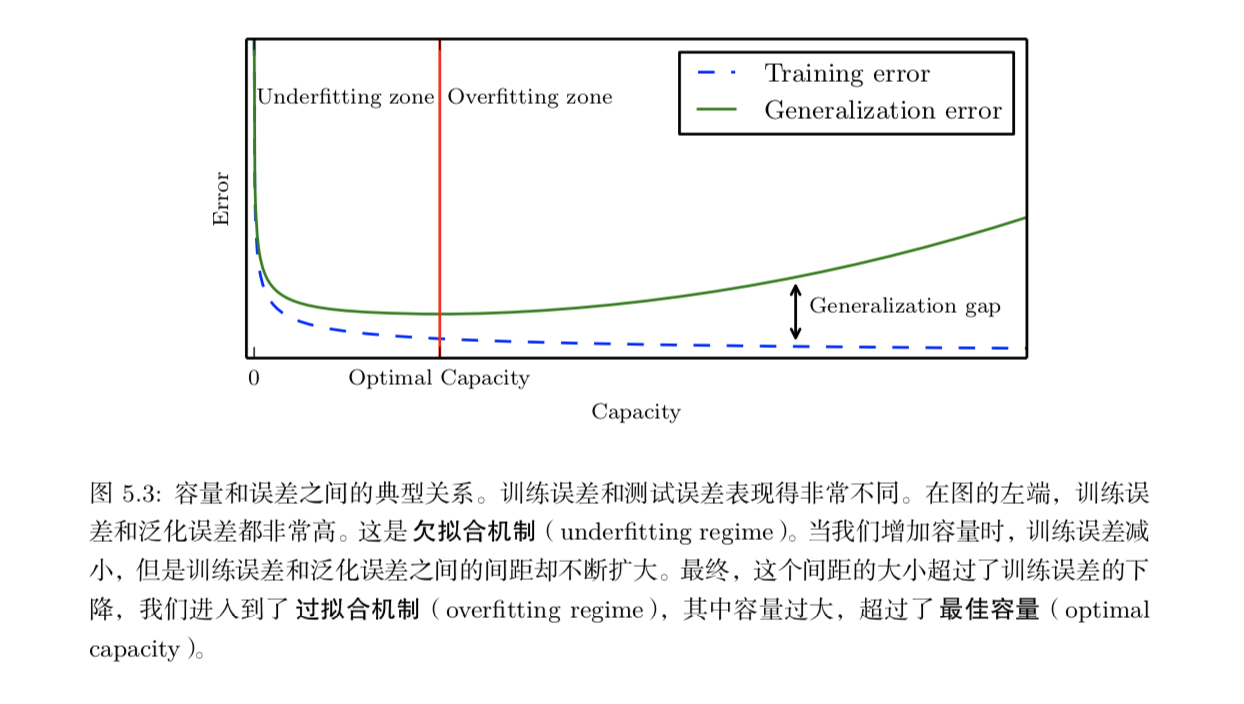
我们必须记住虽然更简单的函数更可能泛化(训练误差和测试误差的差距小)， 但我们仍然需要选择一个充分复杂的假设以达到低的训练误差。通常，当模型容量 上升时，训练误差会下降，直到其渐近最小可能误差(假设误差度量有最小值)。通 常，泛化误差是一个关于模型容量的 U 形曲线函数。

Bayes Error

理想模型假设我们能够预先知道生成数据的真实概率分布。然而这样的模型仍 然会在很多问题上发生一些错误，因为分布中仍然会有一些噪声。在监督学习中，从 x 到 y 的映射可能内在是随机的，或者 y 可能是其他变量(包括 x 在内)的确定性函数。从预先知道的真实分布 p(x, y) 预测而出现的误差被称为 贝叶斯误差(Bayes error)。

No Free Lunch Principle

Linear Regression

正则化

至此，我们具体讨论修改学习算法的方法只有，通过增加或减少学习算法可选 假设空间的函数来增加或减少模型的表示容量。我们列举的一个具体示例是线性回 归增加或减少多项式的次数。目前为止讨论的观点都是过度简化的。

权重衰减

在我们权重衰减的示例中，通过在最小化的目标中额外增加一项，我们明确地 表示了偏好权重较小的线性函数。有很多其他方法隐式或显式地表示对不同解的偏 好。总而言之，这些不同的方法都被称为 正则化(regularization)。正则化是指我们修改学习算法，使其降低泛化误差而非训练误差。正则化是机器学习领域的中心问 题之一，只有优化能够与其重要性相媲。

超参数和验证集

大多数机器学习算法都有超参数，可以设置来控制算法行为。超参数的值不是 通过学习算法本身学习出来的，比如控制权重衰减成都的lamda以及控制容量的多项式最高次数。

有时一个选项被设为学习算法不用学习的超参数，是因为它太难优化了。更多 的情况是，该选项必须是超参数，因为它不适合在训练集上学习。这适用于控制模 型容量的所有超参数。如果在训练集上学习超参数，这些超参数总是趋向于最大可 能的模型容量，导致过拟合(参考图 5.3 )。例如，相比低次多项式和正的权重衰减 设定，更高次的多项式和权重衰减参数设定 λ = 0 总能在训练集上更好地拟合。

为了解决这个问题，我们需要一个训练算法观测不到的 验证集(validation set) 样本。它可以用来估计学 习过程完成之后的学习器的泛化误差。其重点在于测试样本不能以任何形式参与到 模型的选择中，包括设定超参数。基于这个原因，测试集中的样本不能用于验证集。 因此，我们总是从训练数据中构建验证集。特别地，我们将训练数据分成两个不相 交的子集。其中一个用于学习参数。另一个作为验证集，用于估计训练中或训练后 的泛化误差，更新超参数。

Cross Validation

Bias & Variance

偏差和方差度量着估计量的两个不同误差来源。偏差度量着偏离真实函数或参数的误差期望。而方差度量着数据上任意特定采样可能导致的估计期望的偏差。

当我们可以在一个偏差更大的估计和一个方差更大的估计中进行选择时，会发 生什么呢?我们该如何选择?

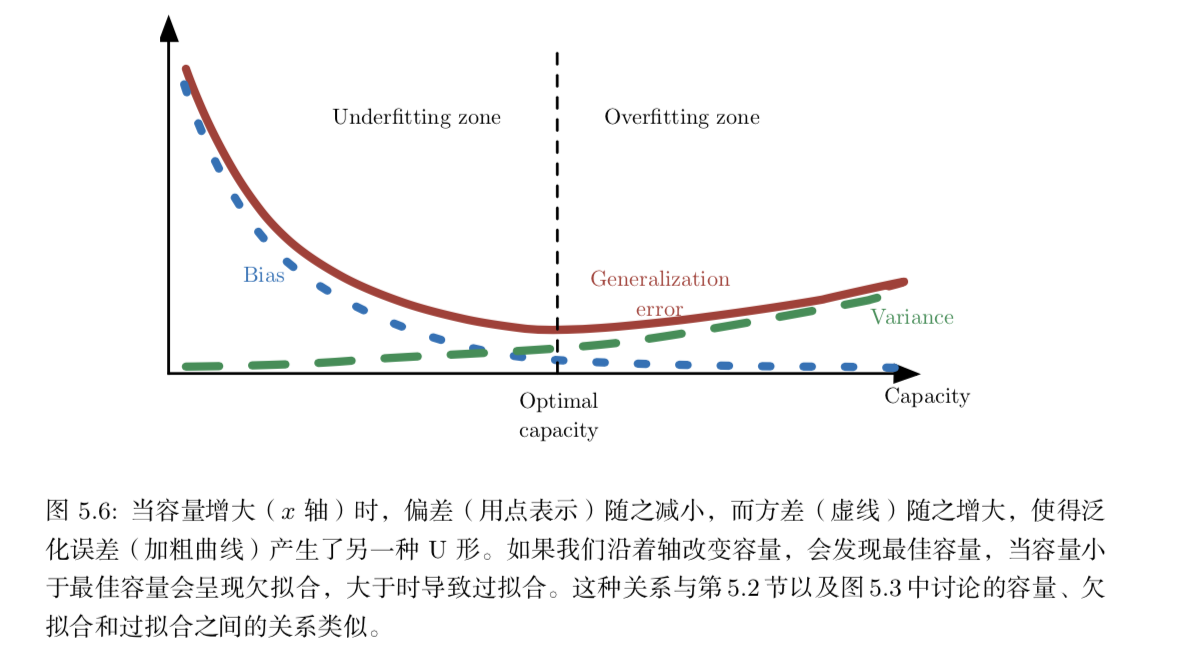
偏差和方差的关系和机器学习容量、欠拟合和过拟合的概念紧密相联。用 MSE 度 量泛化误差(偏差和方差对于泛化误差都是有意义的)时，增加容量会增加方差，降低偏差。如图所示，我们再次在关于容量的函数中，看到泛化误差的 U 形曲线。

Maximum Likelihood

一种解释最大似然估计的观点是将它看作最小化训练集上的经验分布 pˆ_data 和模型分布之间的差异.

Bayes Method

当训练数据很有限时，贝叶斯方法通常泛化得更好，但是当训练样本数目很大 时，通常会有很大的计算代价。

最大后验估计 MAP

Supervised Learning

Linear Regression

Logistic Regression

Support Vector Machine:不输出概率 只输出类别

Kernal Method

Decision Tree

Unsupervised Learning

一个经典的无监督学习任务是找到数据的 ‘‘最佳’’ 表示。‘‘最佳’’ 可以是不同的 表示，但是一般来说，是指该表示在比本身表示的信息更简单或更易访问而受到一 些惩罚或限制的情况下，尽可能地保存关于 x 更多的信息。

有很多方式定义较简单的表示。最常见的三种包括低维表示、稀疏表示和独立 表示。低维表示尝试将 x 中的信息尽可能压缩在一个较小的表示中。稀疏表示将数 据集嵌入到输入项大多数为零的表示中 (Barlow, 1989; Olshausen and Field, 1996; Hinton and Ghahramani, 1997)。稀疏表示通常用于需要增加表示维数的情况，使得 大部分为零的表示不会丢失很多信息。这会使得表示的整体结构倾向于将数据分布 在表示空间的坐标轴上。独立表示试图分开数据分布中变化的来源，使得表示的维 度是统计独立的。

PCA

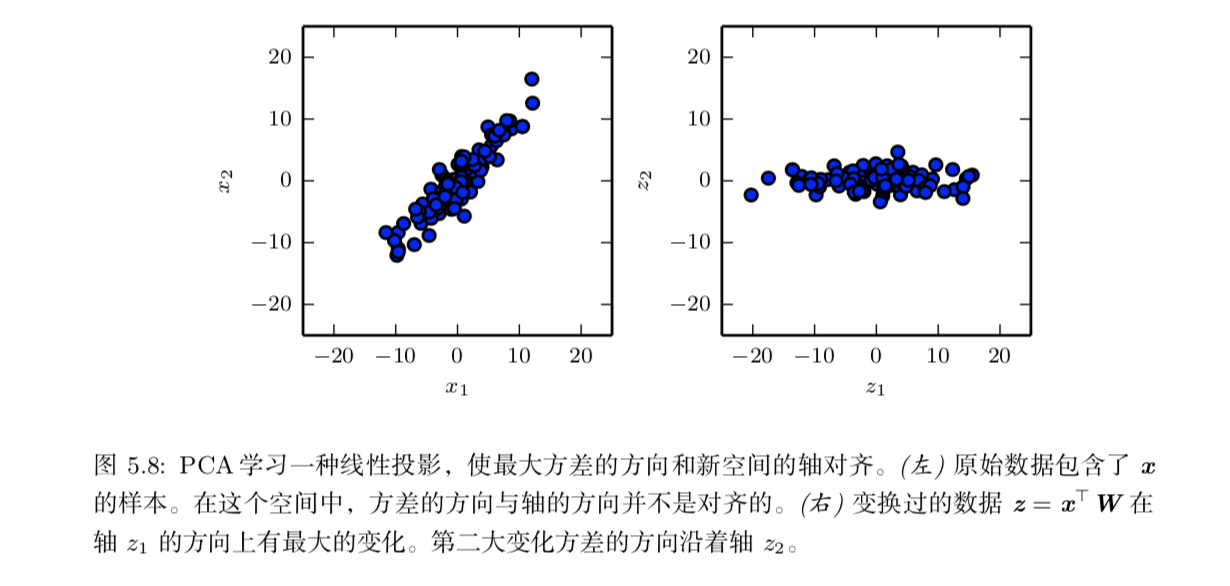
PCA 学习一种比原始输入维数更低的表示。

K均值聚类： K Clustering

随机梯度下降 Stochastic Gradient Descent, SGD

机器学习中反复出现的一个问题是好的泛化需要大的训练集，但大的训练集的 计算代价也更大。

Build a Machine Learning Algorithm

Dimension Disaster