Mathematical Symbols

Introduction

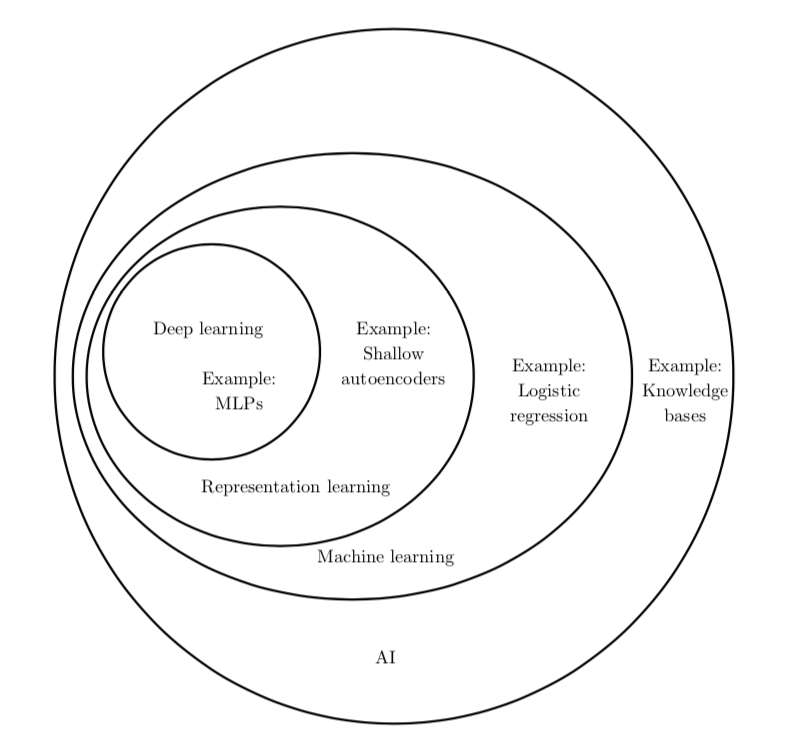
许多人工智能任务都可以通过以下方式解决:先提取一个合适的特征集，然后将这些特征提供给简单的机器学习算法。例如，对于通过声音鉴别说话者的任务来 说，一个有用的特征是对其声道大小的估计。这个特征为判断说话者是男性、女性还是儿童提供了有力线索

然而，对于许多任务来说，我们很难知道应该提取哪些特征。例如，假设我们想 写一个程序来检测照片中的车。我们知道，汽车有轮子，所以我们可能会想用车轮的存在与否作为特征。

解决这个问题的途径之一是使用机器学习来发掘表示本身，而不仅仅把表示映射到输出。这种方法我们称之为表示学习(representation learning)。学习到的表示往往比手动设计的表示表现得更好。并且它们只需最少的人工干预，就能让AI系统迅速适应新的任务。

从原始数据中提取如此高层次、抽象的特征是非常困难的。许多诸如说话口音这样的变差因素，只能通过对数据进行复杂的、接近人类水平的理解来辨识。这几乎与获得原问题的表示一样困难，因此，乍一看，表示学习似乎并不能帮助我们。

深度学习(deep learning)通过其他较简单的表示来表达复杂表示，解决了表示学习中的核心问题。深度学习让计算机通过较简单概念构建复杂的概念。

深度学习的另一个最大的成就是其在 强化学习(reinforcement learning)领域 的扩展。在强化学习中，一个自主的智能体必须在没有人类操作者指导的情况下，通 过试错来学习执行任务。DeepMind 表明，基于深度学习的强化学习系统能够学会玩 Atari 视频游戏，并在多种任务中可与人类匹敌 (Mnih et al., 2015)。深度学习也显 著改善了机器人强化学习的性能 (Finn et al., 2015)。

Linear Algebra

标量Scalar：一个数

向量Vector：一列数

矩阵Matrix：二维数组

A_m,n表示一个高度m宽度n的数组，A_i,: 和A_:,j分别表示row i和column j。

张量Tensor：超过两维的数组，如A_x,y,z

转置Transpose: x^T

对于一个任意形状的矩阵都是可转置的。

矩阵和向量相乘：

C=AB,A的#column等于B的#row。

单位矩阵：I_n(n*n)

任意向量和单位矩阵相乘都不会改变。

逆矩阵：A^-1

A^-1A=I_n

可逆矩阵

一个可逆矩阵必须是一个方阵，即m=n，且所有的列向量都是线性无关的。一个列向量线性相关的矩阵为奇异矩阵（singular）。

范数

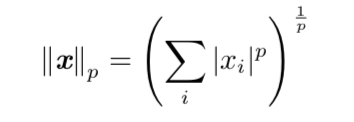
用于衡量一个向量的大小，p belongs to R and p >=1。

p=2:欧几里得范数

p=1:Lasso Regularzation

对角矩阵：diagonal matrix

对称矩阵：A^T=A

单位向量: ||x||₂=1

正交矩阵：orthogonal matrix A^T=A^-1

特征分解

特征向量，指与矩阵 A 相乘后相当于对该向量进行缩放的非零向量 v

Av=lv

（l为特征值）

所有特征值都是正数的矩阵被称为 正定(positive definite);所有特征值都是非 负数的矩阵被称为 半正定(positive semidefinite)。同样地，所有特征值都是负数的 矩阵被称为 负定(negative definite);所有特征值都是非正数的矩阵被称为 半负定(negative semidefinite)。

奇异值分解

A=UDV^T

Moore-Penrose伪逆A⁺

对于非方阵而言，其逆矩阵没有定义。

A⁺=VD⁺U^T

迹Tr(A)=Sum A_i,i

行列式：det(A)

将方阵A映射到实数的函数

Probability

随机变量 Random Variable

概率分布 Probability Distribution

联合概率分布 P(X=x,Y=y)

概率密度函数 Probability Density Function/pdf

边缘概率分布

条件概率: P(Y=y|X=x)=P(Y=y,X=x)/P(X=x)

链式法则

独立性/条件独立性

期望Expectation

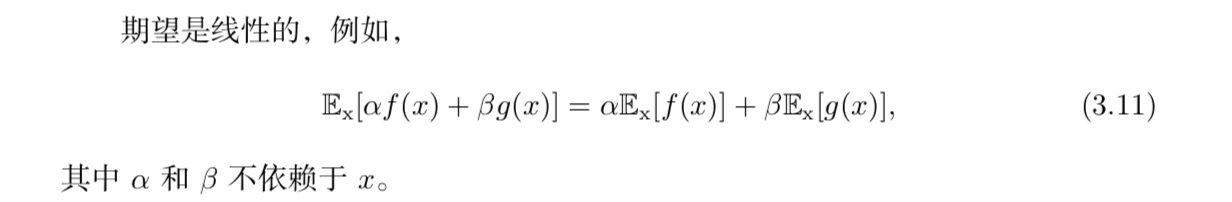
方差

协方差

中心极限定理

logistic sigmoid函数

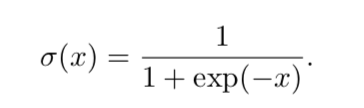
softplus函数

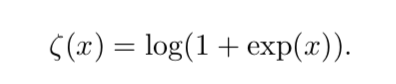
Bayes Rules

P(x|y)=P(x)P(y|x)/P(y)

信息论

KL散度